Amdahlin laki - Amdahl's law

Ohjelman suorituksen viiveen teoreettinen nopeus sen suorittavien suorittimien lukumäärän mukaan Amdahlin lain mukaan. Nopeutta rajoittaa ohjelman sarjaosa. Jos esimerkiksi 95% ohjelmasta voidaan rinnastaa, teoreettinen suurin nopeus rinnakkaislaskennan avulla olisi 20 kertaa.

In tietokone arkkitehtuuri , Amdahlin lain (tai Amdahlin argumentti ) on kaava, joka antaa teoreettinen pyörimisnopeuden on latenssi ja tehtävän suoritus kiinteään työmäärä että voidaan odottaa järjestelmän, jonka resurssit ovat parantuneet. Se on nimetty tietotekniikan tutkija Gene Amdahlin mukaan , ja se esiteltiin AFIPS Spring Joint Computer Conference -tapahtumassa vuonna 1967.

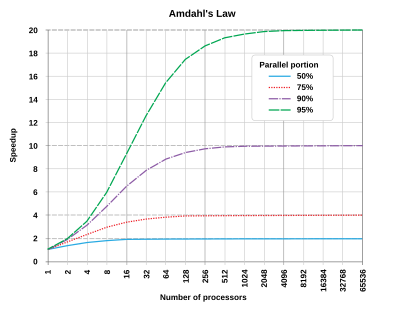
Amdahlin lakia käytetään usein rinnakkaislaskennassa ennustamaan teoreettista nopeutta käytettäessä useita prosessoreita. Jos esimerkiksi ohjelma tarvitsee 20 tuntia suorittaakseen yhden säikeen, mutta yhden tunnin osaa ohjelmasta ei voida rinnastaa, siksi vain jäljellä olevat 19 tuntia ( p = 0,95 ) suoritusaikaa voidaan rinnastaa, sitten riippumatta kuinka monta säiettä on omistettu tämän ohjelman rinnakkaistoteutukselle, suorituksen vähimmäisaika ei saa olla alle tunti. Näin ollen teoreettinen nopeus on rajoitettu enintään 20 -kertaiseen yksittäisen säikeen suorituskykyyn . ${\ displaystyle \ left ({\ dfrac {1} {1-p}} = 20 \ right)}$

Määritelmä

Amdahlin laki voidaan muotoilla seuraavasti:

${\ displaystyle S _ {\ text {latenscy}} (s) = {\ frac {1} {(1-p)+{\ frac {p} {s}}}}}$

missä

• S _latenssi on teoreettinen nopeus koko tehtävän suorittamisessa;
• s on sen tehtävän osan nopeuttaminen, joka hyötyy parannetuista järjestelmäresursseista;
• p on suoritusajan osuus siitä osasta, joka hyötyi alun perin parannetuista resursseista.

Lisäksi,

${\ displaystyle {\ begin {tapauksissa} S _ {\ text {latenscy}} (s) \ leq {\ dfrac {1} {1-p}} \\ [8pt] \ lim \ limits _ {s \ to \ infty } S _ {\ text {latenscy}} (s) = {\ dfrac {1} {1-p}}. \ End {tapaukset}}}$

osoittaa, että koko tehtävän suorittamisen teoreettinen nopeus kasvaa järjestelmän resurssien parantuessa ja että parannuksen laajuudesta riippumatta teoreettista nopeutta rajoittaa aina se tehtävän osa, joka ei voi hyötyä parannuksesta .

Amdahlin laki koskee vain tapauksia, joissa ongelman koko on korjattu. Käytännössä, kun lisää laskentaresursseja tulee saataville, niillä on tapana tottua suurempiin ongelmiin (suurempiin tietojoukkoihin), ja rinnakkaistettavassa osassa käytetty aika kasvaa usein paljon nopeammin kuin luontaisesti sarjatyö. Tässä tapauksessa Gustafsonin laki antaa vähemmän pessimistisen ja realistisemman arvion rinnakkaisesta suorituksesta.

Johtaminen

Tehtävä, jonka suorittaa järjestelmä, jonka resursseja on parannettu alkuperäiseen vastaavaan järjestelmään verrattuna, voidaan jakaa kahteen osaan:

• osa, joka ei hyöty järjestelmän resurssien parantamisesta;
• osa, joka hyötyy järjestelmän resurssien parantamisesta.

Esimerkki on tietokoneohjelma, joka käsittelee tiedostoja levyltä. Osa ohjelmasta voi skannata levyn hakemiston ja luoda luettelon sisäisesti olevista tiedostoista. Tämän jälkeen toinen osa ohjelmasta siirtää jokaisen tiedoston erilliseen säikeeseen käsiteltäväksi. Osaa, joka skannaa hakemiston ja luo tiedostoluettelon, ei voida nopeuttaa rinnakkaisella tietokoneella, mutta tiedostoja käsittelevä osa voi.

Koko tehtävän suoritusaika ennen järjestelmän resurssien parantamista on merkitty . Se sisältää sen osan suoritusajan, joka ei hyötyisi resurssien parantamisesta, ja sen osan, joka hyötyisi siitä. Murto tehtävän suoritusajasta, joka hyötyisi resurssien parantamisesta, on merkitty symbolilla . Tämä koskee siis osaa, joka ei hyötyisi siitä . Sitten: ${\ displaystyle T}$${\ displaystyle p}$${\ displaystyle 1-p}$

${\ displaystyle T = (1-p) T+pT.}$

Resurssien parantamisesta hyötyvän osan toteuttamista nopeuttaa tekijä resurssien parantamisen jälkeen. Näin ollen sen osan toteuttamisaika, joka ei hyöty siitä, pysyy samana, kun taas siitä hyötyvä osa tulee: ${\ displaystyle s}$

${\ displaystyle {\ frac {p} {s}} T.}$

Koko tehtävän teoreettinen suoritusaika resurssien parantamisen jälkeen on sitten: ${\ displaystyle T (s)}$

${\ displaystyle T (s) = (1-p) T+{\ frac {p} {s}} T.}$

Amdahlin laki antaa teoreettisen pyörimisnopeuden on latenssi mukaisessa toiminnassa koko tehtävän kiintein työmäärää${\ displaystyle W}$ , joka tuottaa

${\ displaystyle S _ {\ text {latenscy}} (s) = {\ frac {TW} {T (s) W}} = {\ frac {T} {T (s)}} = {\ frac {1} {1-p+{\ frac {p} {s}}}}.}$

Rinnakkaisohjelmat

Jos 30% suoritusajasta voi tapahtua nopeutettuna, p on 0,3; jos parannus tekee kärsivän osan kaksi kertaa nopeammaksi, s on 2. Amdahlin lain mukaan parannuksen soveltamisen yleinen nopeus on:

${\ displaystyle S _ {\ text {latenscy}} = {\ frac {1} {1-p+{\ frac {p} {s}}} = = {\ frac {1} {1-0,3+{\ frac { 0,3} {2}}}} = 1,18.}$

Oletetaan esimerkiksi, että meille annetaan sarjatehtävä, joka on jaettu neljään peräkkäiseen osaan, joiden suoritusajan prosenttiosuudet ovat p 1 = 0,11 , p 2 = 0,18 , p 3 = 0,23 ja p 4 = 0,48 . Sitten meille kerrotaan, että ensimmäistä osaa ei nopeuteta, joten s 1 = 1 , kun taas toinen osa nopeutetaan 5 kertaa, joten s 2 = 5 , kolmas osa nopeutetaan 20 kertaa, joten s 3 = 20 , ja neljäs osa nopeutuu 1,6 kertaa, joten s 4 = 1,6 . Käyttämällä Amdahlin lakia yleinen nopeus on

${\ displaystyle S _ {\ text {latenscy}} = {\ frac {1} {{\ frac {p1} {s1}}+{\ frac {p2} {s2}}+{\ frac {p3} {s3} }+{\ frac {p4} {s4}}}} = {\ frac {1} {{\ frac {0.11} {1}}+{\ frac {0.18} {5}}+{\ frac {0.23} {20}}+{\ frac {0,48} {1.6}}}} = 2.19.}$

Huomaa, kuinka toisen ja kolmannen osan 5 -kertaiset ja 20 -kertaiset nopeutukset eivät vaikuta suuresti kokonaisnopeuteen, kun neljäs osa (48% suoritusajasta) kiihtyy vain 1,6 -kertaiseksi.

Sarjaohjelmat

Oletetaan, että tehtävä on kaksi itsenäistä osaa, ja B . Osa B kestää noin 25% koko laskennan ajasta. Tekemällä kovasti töitä voi saada tämän osan 5 kertaa nopeammaksi, mutta tämä lyhentää koko laskennan aikaa vain hieman. Sitä vastoin joudut ehkä tekemään vähemmän työtä, jotta osa A toimisi kaksi kertaa nopeammin. Tämä tekee laskennasta paljon nopeampaa kuin osan B optimointi , vaikka osan B nopeus on suurempi suhteessa (5 kertaa verrattuna 2 kertaa).

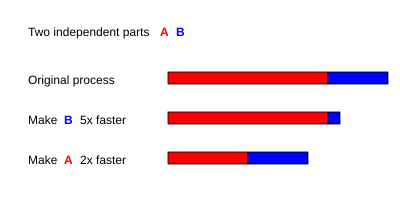
Esimerkiksi sarjaohjelmassa, jossa on kaksi osaa A ja B ja jossa T _A = 3 s ja T _B = 1 s ,

• jos osa B ajetaan 5 kertaa nopeammin, eli s = 5 ja p = T _B /( T _A + T _B ) = 0,25 , niin

${\ displaystyle S _ {\ text {latenscy}} = {\ frac {1} {1-0,25+{\ frac {0,25} {5}}}} = 1,25;}$

• jos osa A suoritetaan 2 kertaa nopeammin, eli s = 2 ja p = T _A /( T _A + T _B ) = 0,75 , niin

${\ displaystyle S _ {\ text {latenscy}} = {\ frac {1} {1-0,75+{\ frac {0,75} {2}}}} = 1,60.}$

Siksi osan A suorittaminen 2 kertaa nopeammaksi on parempi kuin osan B suorittaminen 5 kertaa nopeammaksi. Nopeuden prosentuaalinen parannus voidaan laskea seuraavasti

${\ displaystyle {\ text {prosenttiosuuden parantaminen}} = 100 \ vasen (1-{\ frac {1} {S _ {\ text {latenscy}}}} \ oikea).}$

• Osan A parantaminen kertoimella 2 lisää ohjelman kokonaisnopeutta kertoimella 1,60, mikä tekee siitä 37,5% nopeamman kuin alkuperäinen laskenta.
• Kuitenkin parantamalla B -osaa kertoimella 5, mikä edellyttää oletettavasti enemmän ponnisteluja, saavutetaan vain 1,25 -kertainen nopeuskerroin, mikä tekee siitä 20% nopeamman.

Rinnakkaisohjelmien peräkkäisen osan optimointi

Jos rinnakkaistamaton osa on optimoitu kertoimella , niin ${\ displaystyle O}$

${\ displaystyle T (O, s) = (1-p) {\ frac {T} {O}}+{\ frac {p} {s}} T.}$

Amdahlin laista seuraa, että rinnakkaisuuden aiheuttama nopeus on annettu

${\ displaystyle S _ {\ text {latenscy}} (O, s) = {\ frac {T (O)} {T (O, s)}} = {\ frac {(1-p) {\ frac {1 } {O}}+{p}} {{\ frac {1-p} {O}}+{\ frac {p} {s}}}}.}$

Kun , meillä on , mikä tarkoittaa, että nopeus mitataan suoritusajan suhteen suhteettoman osan optimoinnin jälkeen. ${\ displaystyle s = 1}$${\ displaystyle S _ {\ text {latenscy}} (O, s) = 1}$

Milloin , ${\ displaystyle s = \ infty}$

${\ displaystyle S _ {\ text {latenscy}} (O, \ infty) = {\ frac {T (O)} {T (O, s)}} = {\ frac {(1-p) {\ frac { 1} {O}}+{p}} {{\ frac {1-p} {O}}+{\ frac {p} {s}}}} = 1+{\ frac {p} {1-p }} O.}$

Jos , ja sitten: ${\ displaystyle 1-p = 0,4}$${\ displaystyle O = 2}$${\ displaystyle s = 5}$

${\ displaystyle S _ {\ text {latenscy}} (O, s) = {\ frac {T (O)} {T (O, s)}} = {\ frac {{0.4} {\ frac {1} { 2}}+0,6} {{\ frac {0,4} {2}}+{\ frac {0,6} {5}}}} = 2,5.}$

Rinnakkaisohjelmien peräkkäisten osien muuttaminen rinnastettaviksi

Seuraavaksi tarkastellaan tapausta, jossa rinnakkaistamatonta osaa pienennetään kertoimella ja rinnakkaistettavaa osaa lisätään vastaavasti. Sitten ${\ displaystyle O '}$

${\ displaystyle T '(O', s) = {\ frac {1-p} {O '}} T+\ vasen (1-{\ frac {1-p} {O'}} \ oikea) {\ frac {T} {s}}.}$

Amdahlin laista seuraa, että rinnakkaisuuden aiheuttama nopeus on annettu

${\ displaystyle S '_ {\ text {latenscy}} (O', s) = {\ frac {T '(O')} {T '(O', s)}} = {\ frac {1} { {\ frac {1-p} {O '}}+\ vasen (1-{\ frac {1-p} {O'}} \ oikea) {\ frac {1} {s}}}}.}$

Yllä oleva johtopäätös on yhdenmukainen Jakob Jenkovin analyysin kanssa suoritusajasta vs.

Suhde vähenevän tuoton lakiin

Amdahlin laki sekoitetaan usein pienenevän tuoton lakiin , kun taas vain erityinen tapaus soveltaa Amdahlin lakia osoittaa pienenevän tuoton lain. Jos joku valitsee parhaiten parannetun (saavutetun nopeutuksen kannalta) optimaalisesti, niin paraneminen paranee yksitoikkoisesti. Jos kuitenkin poimitaan ei-optimaalisesti, kun on parannettu alioptimaalista komponenttia ja siirrytään parantamaan optimaalisempaa komponenttia, tuotto voi kasvaa. Huomaa, että on usein järkevää parantaa järjestelmää tässä mielessä "epäoptimaalisessa" järjestyksessä, koska jotkin parannukset ovat vaikeampia tai vaativat enemmän kehitysaikaa kuin toiset.

Amdahlin laki edustaa pienenevän tuoton lakia, jos harkitaan, millaista tuottoa saadaan lisäämällä lisää prosessoreita koneeseen, jos tietokone käyttää kiinteän kokoista laskentaa, joka käyttää kaikkia käytettävissä olevia prosessoreita kapasiteettiinsa nähden. Jokainen järjestelmään lisätty prosessori lisää vähemmän käytettävää virtaa kuin edellinen. Joka kerta, kun kaksinkertaistetaan suorittimien määrä, nopeutussuhde pienenee, kun kokonaisläpäisykyky nousee kohti rajaa 1/(1 -  p ).

Tämä analyysi jättää huomiotta muut mahdolliset pullonkaulat, kuten muistin kaistanleveys ja I/O -kaistanleveys. Jos nämä resurssit eivät skaalaudu prosessorien lukumäärän mukaan, pelkästään prosessorien lisääminen tarjoaa vielä pienemmän tuoton.

Amdahlin lain mukaan seurauksena on, että nopeuttaakseen todellisia sovelluksia, joissa on sekä sarja- että rinnakkaisosia, tarvitaan heterogeenisiä laskentatekniikoita .

Katso myös

• Gustafsonin laki
• Kriittisen polun menetelmä
• Mooren laki

Viitteet

Lue lisää

• Amdahl, Gene M. (1967). "Yhden suorittimen lähestymistavan pätevyys suuren mittakaavan laskentatoimintojen saavuttamiseen" (PDF) . AFIPS -konferenssijulkaisut (30): 483–485. doi : 10.1145/1465482.1465560 .

Ulkoiset linkit

• "Rinnakkaisohjelmointi: Milloin Amdahlin lakia ei voida soveltaa?" . 25.6.2011. Arkistoitu alkuperäisestä päällä 14.4.2013 . Haettu 26.6.2011 .
• Gene M. Amdahl (1989), Oral History haastattelu Gene M. Amdahl , Charles Babbage Institute , University of Minnesota, HDL : 11299/104341. Amdahl keskustelee valmistuneesta työstään Wisconsinin yliopistossa ja WISC: n suunnittelusta . Keskustelee hänen roolistaan ​​useiden IBM: n tietokoneiden suunnittelussa, mukaan lukien STRETCH , IBM 701 ja IBM 704 . Hän keskustelee työstään Nathaniel Rochesterin ja IBM: n suunnitteluprosessin johdon kanssa. Maininnat toimivat Ramo-Wooldridgen , Aeronutronicin ja Computer Sciences Corporationin kanssa
• Amdahlin laki: Kaikki suorituskyvyn parannukset eivät ole tasa -arvoisia (2007)
• "Amdahlin laki" , Joel F.Klein, Wolfram Demonstrations Project (2007)
• Amdahlin laki monisoluisessa aikakaudessa (heinäkuu 2008)
• Mitä $#@! onko rinnakkaisuutta, joka tapauksessa? (Charles Leiserson, toukokuu 2008)
• Arviointi Intel Core i7 Turbo Boost -ominaisuudesta , James Charles, Preet Jassi, Ananth Narayan S, Abbas Sadat ja Alexandra Fedorova (2009)
• Rinnakkaisohjelmien kiihtyvyyden laskeminen säikeiden määrän funktiona , George Popov, Valeri Mladenov ja Nikos Mastorakis (tammikuu 2010)
• Danny Hillis - Amdahlin lain todistaminen vääräksi, video tallennettu lokakuussa 2016