Polynomi -sekvenssi
Chebyshev polynomit ovat kahden sekvenssin polynomien liittyvät kosini ja sini toimintoja, notated kuten ja . Ne voidaan määritellä useilla tavoilla, joilla on sama lopputulos; Tässä artikkelissa polynomit määritellään aloittamalla trigonometrisillä funktioilla :


- Chebyshev polynomi ensimmäisen lajin annetaan


- Määrittele vastaavasti toisen tyyppiset Chebyshevin polynomit muodossa


Nämä määritelmät eivät näytä olevan polynomeja , mutta käyttämällä erilaisia trigonometrisiä identiteettejä ne voidaan muuntaa nimenomaisesti polynomi -muotoon. Esimerkiksi n = 2 T 2 kaava voidaan muuntaa polynomi argumentti x = cos ( θ ) , käyttäen kaksinkertainen kulma on kaava:

Korvaamalla kaavan termit yllä olevilla määritelmillä saamme

Muut T n ( x ) on määritelty samalla tavalla, jossa on polynomien toisen lajin ( U n ) meidän täytyy käyttää de Moivre kaava saada sin ( n θ ) kuin sin ( θ ) kertaa polynomi cos ( θ ) . Esimerkiksi,

antaa

Kun muunnettu polynomi muodossa, T n ( x ) ja U n ( x ) kutsutaan Chebyshev polynomeja ensimmäisen ja toisen lajin , vastaavasti.
Sitä vastoin trigonometristen funktioiden mielivaltainen kokonaislukuteho voidaan ilmaista trigonometristen funktioiden lineaarisena yhdistelmänä käyttäen Chebyshevin polynomeja

jossa alkupiste summasymbolissa osoittaa, että j = 0: n osuus on puolitettava, jos se näkyy, ja .

Tärkeä ja kätevä ominaisuus T n ( x ) on, että ne ovat ortogonaalisia suhteessa sisätulon

ja U n ( x ) ovat ortogonaalisia suhteessa toiseen, analogiseen sisätuotteeseen , joka on esitetty alla. Tämä johtuu siitä, että Chebyshevin polynomit ratkaisevat Chebyshevin differentiaaliyhtälöt


jotka ovat Sturm -Liouvillen differentiaaliyhtälöitä . Tällaisten differentiaaliyhtälöiden yleinen piirre on, että on olemassa erottuva ortonormaali ratkaisuryhmä. (Toinen tapa määritellä Chebyshevin polynomi on näiden yhtälöiden ratkaisut .)
Chebyshev polynomit T n ovat polynomeja, jolla on mahdollisimman johtava kerroin, jonka absoluuttinen arvo on välillä [-1, 1] rajoittuu 1. Ne ovat myös "Esseenin" polynomit monet muut ominaisuudet.
Chebyshev polynomit ovat tärkeitä lähentäminen teoriassa , koska juuret T n ( x ) , joita kutsutaan myös Chebyshev solmut , käytetään vastaavia-pistettä optimoimiseksi polynomi-interpolointi . Tuloksena oleva interpolointipolynomi minimoi Rungen ilmiön ongelman ja antaa likimääräisen arvon, joka on lähellä parasta polynomi -lähentämistä jatkuvalle funktiolle maksiminormin alapuolella , jota kutsutaan myös " minimax " -kriteeriksi. Tämä lähentäminen johtaa suoraan Clenshaw – Curtis -kvadratuurimenetelmään .
Nämä polynomit on nimetty Pafnuty Chebyshevin mukaan . Kirjain T on käytetty, koska vaihtoehtoisen translitteroinnit nimen Tšebyšov kuin Tchebycheff , Tchebyshev (ranskaksi) tai Tschebyschow (saksaksi).
Määritelmät
Toistumisen määritelmä

Juonta ensimmäisen viiden
T n Tšebyšov polynomeiksi ensimmäinen laatuaan
Chebyshev polynomi ensimmäisen lajin saadaan toistuvalla suhteella

Tavallinen generoiva funktio varten T n on

Chebyshevin polynomeille on olemassa useita muita generointitoimintoja ; eksponentiaalinen generoiva funktio on

2-ulotteisen potentiaaliteorian ja moninapaisen laajennuksen kannalta olennainen generointitoiminto on


Kaavio ensimmäisten viiden
U n Chebyshev -polynomin toisesta lajista
Chebyshev polynomi toisen lajin on määritelty toistumisen suhteen

Huomaa, että kaksi differenssiyhtälö ovat identtisiä, paitsi vs. .
Tavallinen U n: n generointitoiminto on



eksponentiaalinen generointitoiminto on

Trigonometrinen määritelmä
Kuten johdannossa on kuvattu, ensimmäisen tyyppiset Chebyshevin polynomit voidaan määritellä ainutlaatuisiksi polynomeiksi, jotka täyttävät

tai toisin sanoen ainutlaatuisina polynomeina, jotka täyttävät

ja n = 0, 1, 2, 3, ... , joka teknisenä piste on variantti (vastaa transpoosia) ja Schröder yhtälön . Se on, T n ( x ) on toiminnallisesti konjugaatin nx , kodifioitu sisäkkäin omaisuutta alla.
Toisen tyyppiset polynomit täyttävät:

tai

joka on rakenteeltaan melko samanlainen kuin Dirichlet -ydin D n ( x ) :

Se, että cos nx on n: n asteen polynomi cos x: ssä, voidaan nähdä havaitsemalla, että cos nx on de Moivren kaavan toisen puolen todellinen osa . Toisen puolen todellinen osa on cos x: n ja sin x: n polynomi , jossa kaikki synnin x voimat ovat parillisia ja siten korvattavissa identiteetin cos 2 x + sin 2 x = 1 kautta . Samalla päättelyllä sin nx on polynomin kuvitteellinen osa, jossa kaikki synnin x tehot ovat parittomia ja siten, jos yksi otetaan huomioon, loput voidaan korvata ( n −1) th asteen polynomin luomiseksi in cos x .
Identiteetti on varsin hyödyllinen rekursiivisen generointikaavan yhteydessä, koska sen avulla voidaan laskea kulman minkä tahansa integraalisen moninkertaisen kosini yksinomaan peruskulman kosinin perusteella.
Kahden ensimmäisen Chebyshev -polynomin arviointi,

ja

sen voi päättää suoraan

ja niin edelleen.
Kaksi välitöntä seurausta ovat koostumuksen identiteetti (tai puolijoukkoa määrittävä sisäkkäinen ominaisuus )

ja kompleksisen eksponentiaalin ilmaisu Chebyshevin polynomeissa: annettu z = a + bi ,

Pell -yhtälön määritelmä
Chebyshevin polynomi voidaan myös määritellä Pell -yhtälön ratkaisuksi

renkaassa R [ x ] . Siten ne voidaan luoda vakiotekniikalla Pell -yhtälöille perusratkaisun valtuuksien ottamiseksi:

Kahdenlaisia Chebyshevin polynomeja koskevat suhteet
Chebyshev polynomi ensimmäisen ja toisen eri vastaavat täydentävä pari Lucas sekvenssien V n ( P , Q ) ja x n ( P , Q ), jossa parametrit P = 2 x ja Q = 1 :

Tästä seuraa, että ne täyttävät myös parin keskinäisen toistumisen yhtälöitä:

Ensimmäisen ja toisen tyypin Chebyshevin polynomeja yhdistävät myös seuraavat suhteet:

Chebyshevin polynomien derivaatan toistumissuhde voidaan johtaa näistä suhteista:

Tätä suhdetta käytetään Chebyshevin spektrimenetelmässä differentiaaliyhtälöiden ratkaisemiseksi.
Turánin eriarvoisuus Chebyshevin polynomeissa on

Integraaliset suhteet ovat

jossa integraaleja pidetään pääarvona.
Selkeät ilmaisut
Erilaiset lähestymistavat Chebyshevin polynomien määrittämiseen johtavat erilaisiin ilmaisuihin, kuten:

käänteisellä

jossa alkupiste summasymbolissa osoittaa, että j = 0: n osuus on puolitettava, jos se näkyy.

jossa 2 F 1 on hypergeometrinen funktio .
Ominaisuudet
Symmetria

Toisin sanoen parillisen tason Chebyshevin polynomeilla on tasasymmetria ja ne sisältävät vain parillisia x: n voimia . Parittoman järjestyksen Chebyshevin polynomeilla on pariton symmetria ja ne sisältävät vain x: n parittomia voimia .
Juuret ja ääriliikkeet
Kummankin tyyppisellä Chebyshevin polynomilla, jonka aste on n, on n eri yksinkertaista juurta, joita kutsutaan Chebyshevin juuriksi , aikavälillä [−1, 1] . Ensimmäisen tyyppisen Chebyshev -polynomin juuria kutsutaan joskus Chebyshev -solmuiksi, koska niitä käytetään solmuina polynomi -interpoloinnissa. Käyttämällä trigonometristä määritelmää ja sitä, että

voidaan osoittaa, että juuret T n ovat

Samoin U n: n juuret ovat

Ääriarvot on T n on välillä -1 ≤ x ≤ 1 sijaitsevat

Yksi ensimmäisen tyyppisten Chebyshev -polynomien ainutlaatuinen ominaisuus on, että aikavälillä −1 ≤ x ≤ 1 kaikilla ääripäillä on arvot, jotka ovat joko -1 tai 1. Näin ollen näillä polynoomeilla on vain kaksi äärellistä kriittistä arvoa . Shabatin polynomit . Sekä ensimmäisessä että toisessa Chebyshev -polynomin tyypissä on päätepisteissä ääripää, jonka antavat:




Eriyttäminen ja integraatio
Polynomien johdannaiset voivat olla vähemmän kuin yksinkertaisia. Erottamalla polynomit niiden trigonometrisissä muodoissa voidaan osoittaa, että:

Kaksi viimeistä kaavaa voivat olla numeerisesti hankalia, koska ne jaetaan nollalla (0/0 määrittämätön muoto , erityisesti) kohdissa x = 1 ja x = −1 . Voidaan osoittaa, että:

|
Todiste
|
|
Ensimmäinen Chebyshevin polynomin toinen johdannainen on

joka edellä kuvatulla tavalla arvioituna aiheuttaa ongelman, koska se on määrittämätön kohdassa x = ± 1 . Koska funktio on polynomi, (kaikkien) johdannaisten on oltava olemassa kaikille reaaliluvuille, joten yllä olevan lausekkeen rajoittamisen pitäisi antaa haluttu arvo:

jossa vain x = 1 otetaan huomioon. Nimittäjän tekijä:

Koska rajan kokonaisuutena on oltava olemassa, lukijan ja nimittäjän rajan on oltava itsenäisesti olemassa, ja

Nimittäjä (edelleen) rajoittuu nollaan, mikä tarkoittaa sitä, että osoittimen on rajoituttava nollaan eli U n - 1 (1) = nT n (1) = n, josta on hyötyä myöhemmin. Koska lukija ja nimittäjä ovat molemmat nollarajoja, sovelletaan L'Hôpitalin sääntöä :

Todiste x = −1 on samanlainen, sillä T n (−1) = (−1) n on tärkeä.
|
Yleisempi kaava sanoo:

josta on suurta hyötyä ominaisarvoon liittyvien ongelmien numeerisessa ratkaisussa.
Lisäksi meillä on

jossa alkupiste summasymboleissa tarkoittaa, että termi k = 0 on puolitettava, jos se esiintyy.
Koskevat integraatio, ensimmäinen derivaatta T n merkitsee sitä, että

ja johdannaisia sisältävien ensimmäisen tyyppisten polynomien toistosuhde vahvistaa, että n ≥ 2

Viimeinen kaava voidaan lisäksi manipuloida ilmaista integraali T n funktiona Chebyshev polynomi ensimmäisen lajin vain:

Lisäksi meillä on

Chebyshevin polynomien tuotteet
Chebyshevin polynomien kanssa työskennellessä esiintyy usein kahden niistä tuotteita. Nämä tuotteet voidaan pienentää yhdistelmiksi Chebyshevin polynomeista, joilla on alempi tai korkeampi aste, ja lopputulokset tuotteesta on helpompi tehdä. Oletetaan, että seuraavassa indeksi m on suurempi tai yhtä suuri kuin indeksi n ja n ei ole negatiivinen. Ensimmäisen tyyppisten Chebyshevin polynomien osalta tuote laajenee

joka on analogia lisäyslauseelle

identiteettien kanssa

Jos n = 1, tuloksena on jo tunnettu toistumiskaava, joka on vain järjestetty eri tavalla, ja kun n = 2, se muodostaa toistosuhteen kaikille parillisille tai kaikille parittomille Chebyshev -polynomeille (riippuen alimman m : n pariteetista ), mikä mahdollistaa toimintojen suunnittelun määrätyillä symmetriaominaisuuksilla. Tästä tuotelaajennuksesta voidaan päätellä kolme muuta hyödyllistä kaavaa Chebyshevin polynomien arvioimiseksi:

Toisen tyyppisille Chebyshevin polynomeille tuotteet voidaan kirjoittaa seuraavasti:

ja m ≥ n .
Tällä tavoin, kuten edellä, n = 2, toisentyyppisten Chebyshevin polynomien toistumiskaava pienentää molempien symmetriatyyppien

riippuen siitä, alkaako m 2: lla vai 3: lla.
Ortogonaalisuus
Sekä T n ja U: n sekvenssin muodostamiseksi ortogonaaliset polynomit . Polynomien ensimmäisen lajin T n ovat ortogonaalisia suhteessa painoon

aikavälillä [−1, 1] , eli meillä on:

Tämä voidaan todistaa antamalla x = cos θ ja käyttämällä määrittävää identiteettiä T n (cos θ ) = cos nθ .
Samoin polynomit toisen lajin U n ovat ortogonaalisia suhteessa painoon

aikavälillä [−1, 1] , eli meillä on:

(Mitta √ 1 - x 2 d x on normalisointivakion sisällä Wignerin puoliympyrän jakauma .)
T n lisäksi täytettävä erillinen orthogonality ehto:

jossa N on mikä tahansa kokonaisluku, joka on suurempi kuin max ( i , j ) , ja x k ovat T N ( x ) : n N Chebyshev -solmut (katso edellä ) :

Toisenlaisia polynomeja ja kaikkia kokonaislukuja N > i + j, joilla on samat Chebyshev -solmut x k , on samanlaisia summia:

ja ilman painotoimintoa:

Kaikille kokonaisluvuille N > i + j , jotka perustuvat U N ( x ) N -nollaan :

voi saada summan:

ja jälleen ilman painotoimintoa:

Minimaalinen ∞ -norm
Mille tahansa n ≥ 1 , asteen n polynomien joukosta, joilla on johtava kerroin 1 ( monipolynoomit ),

on se, jonka välin [−1, 1] suurin absoluuttinen arvo on minimaalinen.
Tämä suurin absoluuttinen arvo on

ja | f ( x ) | saavuttaa tämän maksimin täsmälleen n + 1 kertaa

|
Todiste
|
|
Oletetaan, että w n ( x ) on asteen n polynomi, jonka johtava kerroin 1 ja jonka suurin absoluuttinen arvo aikavälillä [−1,1] on alle 1/2 n - 1 .
Määritellä

Koska ääripisteiden T n olemme

Alkaen väliarvo lause , f n ( x ) on vähintään n juuria. Tämä on kuitenkin mahdotonta, koska f n ( x ) on asteen n - 1 polynomi , joten algebran peruslause viittaa siihen, että sillä on korkeintaan n - 1 juuria.
|
- Huomautus
Jonka Equioscillation lause , joukossa kaikki polynomit aste ≤ n , polynomi f minimoi || f || ∞ päällä [−1,1] silloin ja vain, jos on n + 2 pistettä −1 ≤ x 0 < x 1 <⋯ < x n + 1 ≤ 1 siten, että | f ( x i ) | = || f || ∞ .
Tietenkin välin [−1,1] nollapolynomi voidaan lähestyä itsestään ja minimoida ∞ -normaali.
Yllä kuitenkin | f | saavuttaa maksiminsa vain n + 1 kertaa, koska etsimme parasta asteen n ≥ 1 polynomia (siksi aiemmin esitettyä teoriaa ei voida käyttää).
Muut ominaisuudet
Chebyshevin polynomit ovat erikoistapaus ultrasfäärisistä tai Gegenbauer -polynomeista , jotka itsessään ovat Jacobin polynomien erityistapaus :

Jokainen positiivinen kokonaisluku n , T n ( x ) ja U n ( x ) ovat molemmat asteluku on n . Ne ovat parillinen tai pariton toiminnot on x , kuten n on parillinen tai pariton, niin silloin, kun kirjoitetaan polynomit x , se vain on parillinen tai pariton asteen termejä vastaavasti. Itse asiassa,

ja

Johtava kerroin on T n on 2 n - 1 , jos 1 ≤ n , mutta 1, jos 0 = n .
T n ovat Lissajous -käyrien erityistapaus,jonka taajuussuhde on n .
Useat polynomisekvenssit, kuten Lucasin polynomi ( L n ), Dicksonin polynomi ( D n ), Fibonaccin polynomi ( F n ), liittyvät Chebyshevin polynomeihin T n ja U n .
Ensimmäisen tyyppiset Chebyshevin polynomit täyttävät suhteen

joka on helposti todistettavissa kosinin tuote-summa-kaavasta . Toisen tyyppiset polynomit täyttävät samanlaisen suhteen

(määritelmän mukaan U −1 ≡ 0 sopimuksen mukaan).
Samanlainen kuin kaava

meillä on vastaava kaava

For X ≠ 0 ,

ja

mikä johtuu siitä, että tämä pätee määritelmän mukaan x = e iθ .
Määritellä

Sitten C n ( x ) ja C m ( x ) ovat työmatkapolynomeja:

kuten käy ilmi edellä määritellystä Abelin pesimäominaisuudesta .
Yleistetyt Chebyshevin polynomit
Yleistetty Chebyshev polynomit T määritellään

jossa a ei ole välttämättä kokonaisluku ja 2 F 1 ( a , b ; c ; z ) on Gaussin hypergeometrinen funktio ; esimerkkinä , . Power -sarjan laajennus


yhtyy .![x \ in [-1,1]](https://wikimedia.org/api/rest_v1/media/math/render/svg/1f9d0dda56ce3e01e14570ac9aef0021c6125722)
Esimerkkejä
Ensimmäinen laji

Ensimmäiset ensimmäiset Chebyshevin polynomit alueella
-1 < x <1 : Tasainen
T 0 ,
T 1 ,
T 2 ,
T 3 ,
T 4 ja
T 5 .
Ensimmäiset ensimmäiset Chebyshevin polynomit ovat OEIS : A028297

Toinen laji
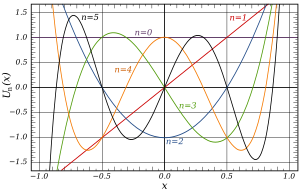
Muutamat ensimmäiset toisen tyyppiset Chebyshev -polynomit alueella
-1 < x <1 : Tasainen
U 0 ,
U 1 ,
U 2 ,
U 3 ,
U 4 ja
U 5 . Vaikka se ei näy kuvassa,
U n (1) = n + 1 ja
U n (−1) = ( n + 1) ( - 1) n .
Ensimmäiset toisen tyyppiset Chebyshevin polynomit ovat OEIS : A053117

Perusasetuksena

Ei-sileä funktio (ylhäällä)
y = -x 3 H ( -x ) , jossa
H on
Heaviside-askelfunktio , ja (alhaalla) sen Chebyshev-laajennuksen viides osa. Kaavion resoluutiolla seitsemäs summa on erottamaton alkuperäisestä funktiosta.
Sopivassa Sobolev tila , joukko Chebyshev polynomeja muodostaa ortonormaali kanta , niin että toimivat samassa tilassa voi, on -1 ≤ x ≤ 1 ekspressoida laajennus:

Lisäksi, kuten aiemmin mainittiin, Chebyshevin polynomi muodostaa ortogonaalisen perustan, joka (muun muassa) merkitsee sitä, että kertoimet a n voidaan määrittää helposti käyttämällä sisäistä tuotetta . Tätä summaa kutsutaan Chebyshev -sarjaksi tai Chebyshev -laajennukseksi .
Koska Chebyshev -sarja liittyy Fourier -kosinisarjaan muuttujien muutoksen kautta, kaikilla Fourier -sarjaa koskevilla lauseilla, identiteeteillä jne. On Chebyshev -vastine. Näitä ominaisuuksia ovat:
- Chebyshevin polynomi muodostaa täydellisen ortogonaalisen järjestelmän.
- Chebyshev -sarja muuttuu f ( x ): ksi, jos toiminto on kappaleittain sileä ja jatkuva . Sileysvaatimusta voidaan lieventää useimmissa tapauksissa - niin kauan kuin f ( x ): ssä ja sen johdannaisissa on rajallinen määrä keskeytyksiä .
- Epäjatkuvuudessa sarja lähenee oikean ja vasemman rajan keskiarvoa.
Fourier -sarjasta perittyjen teoreemien ja identiteettien runsaus tekee Chebyshevin polynomeista tärkeitä työkaluja numeerisessa analyysissä ; ne ovat esimerkiksi suosituimpia yleiskäyttöisiä perustoimintoja, joita käytetään spektrimenetelmässä , usein trigonometristen sarjojen hyväksi, koska jatkuvien funktioiden yleisesti lähentyminen on nopeampaa ( Gibbsin ilmiö on edelleen ongelma).
Esimerkki 1
Harkitse lokin Chebyshev -laajennusta (1 + x ) . Voidaan ilmaista

Kertoimet a n voidaan löytää joko käyttämällä sisäistä tuotetta tai erillistä ortogonaalisuutta. Sisäisen tuotteen osalta

joka antaa

Vaihtoehtoisesti, kun arvioitavan funktion sisäistä tuloa ei voida arvioida, diskreetti ortogonaalisuusehto antaa usein hyödyllisen tuloksen likimääräisille kertoimille,

jossa δ ij on Kroneckerin delta -funktio ja x k ovat N Gauss – Chebyshev -nollia T N ( x ) :

Mille tahansa N : lle nämä likimääräiset kertoimet antavat tarkan likimääräisen arvon x k: n funktiolle, jossa on hallittu virhe näiden pisteiden välillä. Tarkat kertoimet saadaan, kun N = ∞ , mikä edustaa funktiota tarkasti kaikissa [−1,1]: n kohdissa . Lähentymisnopeus riippuu toiminnosta ja sen sujuvuudesta.
Tämän avulla voimme laskea likimääräiset kertoimet a n erittäin tehokkaasti diskreetin kosinimuunnoksen avulla

Esimerkki 2
Toinen esimerkki:

Osittaisia summia
Osasummat

ovat erittäin hyödyllisiä eri toimintojen lähentämisessä ja differentiaaliyhtälöiden ratkaisussa (katso spektrimenetelmä ). Kaksi yleistä menetelmää kertoimien a n määrittämiseksi on käyttää sisäistä tuotetta kuten Galerkinin menetelmässä ja käyttämällä kollokatiota, joka liittyy interpolointiin .
Interpolantina ( N - 1) osasumman N -kertoimet saadaan yleensä Chebyshev – Gauss – Lobatto -pisteistä (tai Lobatto -ruudukosta), mikä johtaa vähimmäisvirheeseen ja välttää Rungen ilmiön, joka liittyy yhtenäiseen verkkoon. Tämä pisteiden kokoelma vastaa summan korkeimman kertaluvun polynomin ääripäätä ja päätepisteet, ja sen antaa:

Polynomi Chebyshevin muodossa
Mielivaltainen asteen N polynomi voidaan kirjoittaa ensimmäisen tyyppisten Chebyshev -polynomien muodossa. Tällainen polynomi p ( x ) on muotoa

Tšebyshev -muotoisia polynomeja voidaan arvioida Clenshaw -algoritmin avulla .
Siirtynyt Chebyshevin polynomi
Ensimmäisen tyyppiset siirretyt Chebyshevin polynomit määritellään

Kun Chebyshev -polynomin argumentti on alueella 2 x - 1 ∈ [−1, 1] , siirretyn Chebyshev -polynomin argumentti on x ∈ [0, 1] . Samoin voidaan määrittää siirrettyjä polynomeja yleisille aikaväleille [ a , b ] .
Katso myös
Viitteet
Lähteet
-
Abramowitz, Milton ; Stegun, Irene Ann , toim. (1983) [kesäkuu 1964]. "Luku 22" . Matemaattisten funktioiden käsikirja kaavojen, kaavioiden ja matemaattisten taulukoiden kanssa . Sovelletun matematiikan sarja. 55 (yhdeksäs uusintapainos, jossa on lisäkorjauksia kymmenennestä alkuperäisestä painoksesta ja korjaukset (joulukuu 1972); ensimmäinen toim.). Washington DC; New York: Yhdysvaltain kauppaministeriö, National Bureau of Standards; Doverin julkaisut. s. 773. ISBN 978-0-486-61272-0. LCCN 64-60036 . MR 0167642 . LCCN 65-12253 .
-
Dette, Holger (1995). "Huomautus eräistä erikoisista epälineaarisista äärimmäisistä ilmiöistä Chebyshevin polynomeissa". Edinburghin matemaattisen seuran julkaisut . 38 (2): 343–355. arXiv : matematiikka/9406222 . doi : 10.1017/S001309150001912X . S2CID 16703489 .
-
Elliott, David (1964). "Funktion Chebyshev -sarjan laajennuksen kertoimien arviointi ja arviointi" . Matematiikka. Comp . 18 (86): 274–284. doi : 10.1090/S0025-5718-1964-0166903-7 . MR 0166903 .
-
Eremenko, A .; Lempert, L. (1994). "Äärimmäinen ongelma polynomeille" (PDF) . American Mathematical Societyn julkaisut . 122 (1): 191–193. doi : 10.1090/S0002-9939-1994-1207536-1 . MR 1207536 .
-
Hernandez, MA (2001). "Chebyshevin likimääräiset algoritmit ja sovellukset" . Comp. Matematiikka. Sovellukset . 41 (3–4): 433–445. doi : 10.1016/s0898-1221 (00) 00286-8 .
-
Mason, JC (1984). "Jotkut Chebyshevin polynomin ominaisuudet ja sovellukset ja järkevä lähentäminen". Järkevä lähentäminen ja interpolointi . Luennon muistiinpanoja matematiikassa. 1105 . s. 27–48. doi : 10.1007/BFb0072398 . ISBN 978-3-540-13899-0.
-
Mason, JC; Handscomb, DC (2002). Chebyshev Polynomials . Taylor & Francis.
-
Mathar, RJ (2006). "Käänteisten polynomien Chebyshev -sarjan laajennus". J. Comput. Appl. Matematiikka . 196 (2): 596–607. arXiv : matematiikka/0403344 . Bibcode : 2006JCoAM.196..596M . doi : 10.1016/j.cam.2005.10.013 . S2CID 16476052 .
-
Koornwinder, Tom H .; Wong, Roderick SC; Koekoek, Roelof; Swarttouw, René F. (2010), "Orthogonal Polynomials" , julkaisussa Olver, Frank WJ ; Lozier, Daniel M .; Boisvert, Ronald F .; Clark, Charles W. (toim.), NIST Handbook of Mathematical Functions , Cambridge University Press, ISBN 978-0-521-19225-5, MR 2723248
-
Remes, Eugene. "Chebyshev Polynomialsin äärimmäisestä omaisuudesta" (PDF) .
-
Salzer, Herbert E. (1976). "Muuntaa interpolointisarjat Chebyshev -sarjoiksi toistoskaavoilla" . Matematiikka. Comp . 30 (134): 295–302. doi : 10.1090/S0025-5718-1976-0395159-3 . MR 0395159 .
-
Scraton, RE (1969). "Integraaliyhtälöiden ratkaisu Chebyshev -sarjassa" . Matematiikka. Tietokone . 23 (108): 837–844. doi : 10.1090/S0025-5718-1969-0260224-4 . MR 0260224 .
-
Smith, Lyle B. (1966). "Chebyshev -sarjan kertoimien laskeminen". Comm. ACM . 9 (2): 86–87. doi : 10.1145/365170.365195 . S2CID 8876563 . Algoritmi 277.
-
Suetin, PK (2001) [1994], "Chebyshevin polynomi" , Encyclopedia of Mathematics , EMS Press
Ulkoiset linkit

 Mediat, jotka liittyvät Chebyshevin polynomeihin Wikimedia Commonsissa
Mediat, jotka liittyvät Chebyshevin polynomeihin Wikimedia Commonsissa









































































































![x \ in [-1,1]](https://wikimedia.org/api/rest_v1/media/math/render/svg/1f9d0dda56ce3e01e14570ac9aef0021c6125722)















