Säännöllinen polytooppi - Regular polytope
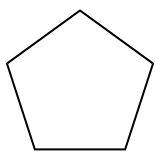 Tavallinen viisikulmio on monikulmio , kaksiulotteinen polytooppi, jossa on 5 reunaa ja jota edustaa Schläfli-symboli {5}. |
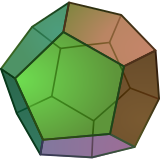 Tavallinen dodekahedroni on polyhedron , kolmiulotteinen polytooppi, jossa on 12 viisikulmaista pintaa , joita edustaa Schläfli-symboli {5,3}. |
 Säännöllinen 120-solu on polychoron , neljän ulotteinen polytooppia, 120 dodekahedraalisia solujen , jota edustaa Schläfli symboli {5,3,3}. (tässä Schlegel-kaaviona ) |
 Säännöllinen kuutioinen hunajakenno on tessellaatio , ääretön kolmiulotteinen polytooppi, jota edustaa Schläfli-symboli {4,3,4}. |
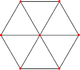
 8-kuution 256 kärkeä ja 1024 reunaa voidaan näyttää tässä kohtisuorassa projektiossa ( Petrie-polygoni ) |
|
Vuonna matematiikka , joka on säännöllinen polytooppi on polytooppi jonka symmetria ryhmä toimii transitiivisesti sen lippua , mikä antaa sille mahdollisimman suurta symmetriaa. Kaikki sen elementit tai j- kasvot (kaikille 0 ≤ j ≤ n , missä n on polytoopin ulottuvuus) - solut, kasvot ja niin edelleen - ovat myös transitiivisia polytoopin symmetrialla ja ovat säännöllisiä ulottuvuuden ≤ polytooppeja n .
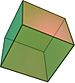
Säännölliset polytoopit ovat yleistynyt analogia missä tahansa määrin säännöllisten polygonien (esimerkiksi neliön tai säännöllisen viisikulmion) ja säännöllisten polyhedrien (esimerkiksi kuution ) ulottuvuuksia . Säännöllisten polytooppien voimakas symmetria antaa heille esteettisen laadun, joka kiinnostaa sekä ei-matemaatikkoja että matemaatikkoja.
Klassisesti säännöllinen polytooppi n ulottuvuudessa voidaan määritellä siten, että sillä on säännölliset puolet [( n - 1) -kasvot] ja säännölliset huippupisteet . Nämä kaksi ehtoa ovat riittävät varmistamaan, että kaikki kasvot ovat samanlaiset ja kaikki kärjet ovat samanlaiset. Huomaa kuitenkin, että tämä määritelmä ei toimi abstraktien polytooppien kohdalla .
Säännöllinen polytooppi voidaan esittää Schläfli-symbolilla , jonka muoto on {a, b, c, ...., y, z}. Säännölliset puolet ovat {a, b, c, ..., y} ja säännölliset. kärjen luvut muodossa {b, c, ..., y, z}.
Luokitus ja kuvaus
Säännölliset polytoopit luokitellaan ensisijaisesti niiden ulottuvuuden mukaan.
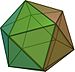
Ne voidaan edelleen luokitella symmetrian mukaan . Esimerkiksi kuutiolla ja tavallisella oktaedrilla on sama symmetria kuin tavallisella dodekaedrillä ja ikosaedrilla . Symmetriaryhmät nimetään joskus säännöllisten polytooppien, esimerkiksi tetraedristen ja ikosaedristen symmetrioiden, mukaan.
Jokaisessa ulottuvuudessa on kolme säännöllisen polytoopin erikoisluokkaa:
- Säännöllinen yksisuuntainen
- Mittaa polytooppi (Hypercube)
- Ristipolytooppi (Orthoplex)
Kahdessa ulottuvuudessa on äärettömän paljon säännöllisiä polygoneja . Kolme ja neljä ulottuvuutta, näiden kolmen lisäksi on useita säännöllisempiä polyhedraa ja 4-polytooppeja . Viidessä ulottuvuudessa ja enemmän nämä ovat ainoat. Katso myös luettelo tavallisista polytoopeista .
Polytoopin ajatus on joskus yleistetty sisällyttämään siihen liittyviä geometrisia esineitä. Joillakin näistä on säännöllisiä esimerkkejä, kuten alla olevassa historiallisia löytöjä käsittelevässä osiossa käsitellään.
Schläfli-symbolit
Ludwig Schläfli kehitti 1800-luvulla tiiviin symbolisen esityksen tavallisille polytoopeille , ja hieman muunnetusta muodosta on tullut vakio. Merkinnät voidaan parhaiten selittää lisäämällä yksi ulottuvuus kerrallaan.
- Kupera säännöllinen monikulmio , jossa on n sivut on merkitty { n }. Joten tasasivuinen kolmio on {3}, neliö {4} ja niin edelleen loputtomiin. Säännöllistä tähden monikulmiota, joka kääntyy m kertaa keskikohdan ympärillä, merkitään murto-arvolla { n / m }, jossa n ja m ovat yhtä alkupäätä , joten säännöllinen pentagrammi on {5/2}.
- Säännöllinen monitahokas , jossa pinnat { n }, jossa p kasvot liittyä noin kärkipiste merkitään { n , s }. Yhdeksän tavallista polyhedraa ovat {3, 3} {3, 4} {4, 3} {3, 5} {5, 3} {3, 5/2} {5/2, 3} {5, 5/2 } ja {5/2, 5}. { P } on kärkipiste luku polyhedroni.
- Säännöllistä 4-polytooppia, jossa solut { n , p } ja q- solut yhdistyvät reunan ympäri, merkitään { n , p , q }. 4-polytoopin kärkiluku on { p , q }.
- Säännöllinen 5-polytooppi on { n , p , q , r }. Ja niin edelleen.
Säännöllisten polytooppien kaksinaisuus
Kahden säännöllisen polytooppi Myös säännöllinen polytooppia. Kaksoispolytoopin Schläfli-symboli on vain taaksepäin kirjoitettu alkuperäinen symboli: {3, 3} on itsekaksoinen, {3, 4} on kaksoismerkki {4, 3}, {4, 3, 3} - {3, 3, 4} ja niin edelleen.
Kärki luku säännöllinen polytooppi on kaksi dual polytooppi n puoli. Esimerkiksi kohdan {3, 3, 4} kärkiluku on {3, 4}, jonka kaksoisarvo on {4, 3} - solun {4, 3, 3}.
Toimenpiteen ja syötön polytooppeina tahansa ulottuvuus on kaksi toisiaan.
Jos Schläfli-symboli on palindrominen , ts. Lukee samaa eteen- ja taaksepäin, polyhedron on itsekaksoinen. Itsekaksoiset säännölliset polytoopit ovat:
- Kaikki säännölliset polygonit , {a}.
- Kaikki tavalliset n - yksinkertaisuudet , {3,3, ..., 3}
- Tavallinen 24-solu 4 ulottuvuudessa, {3,4,3}.
- Suuri 120-solujen ({5,5 / 2,5}) ja grand stellated 120-solujen ({5 / 2,5,5 / 2}) 4 mitat.
- Kaikki tavalliset n- ulotteiset kuutiomaiset hunajakennot , {4,3, ..., 3,4}. Näitä voidaan käsitellä loputtomina polytooppeina .
- Hyperboliset laatat ja kennot (laatat {p, p} p> 4 2-ulotteisina, {4,4,4} , {5,3,5} . {3,5,3} , {6,3,6} ja {3,6,3} 3 ulottuvuudessa, {5,3,3,5} 4 ulottuvuudessa ja {3,3,4,3,3} 5 ulottuvuudessa).
Säännölliset yksinkertaistukset

|

|

|

|
| Jana | Kolmio | Tetrahedron | Pentachoron |

|

|

|
Aloittaa seikasta . Merkitse piste B etäisyydelle r siitä ja yhdistä muodostaaksesi viivasegmentin . Merkitse piste C toisessa, kohtisuorassa ulottuvuudessa etäisyydellä r molemmista, ja liity A: han ja B : hen muodostaaksesi tasasivuisen kolmion . Merkitse piste D kolmannessa, kohtisuorassa, mitoita etäisyys r kaikista kolmesta ja yhdistä muodostaaksesi säännöllisen tetraedrin . Ja niin korkeammille ulottuvuuksille.
Nämä ovat tavallisia yksinkertaistuksia tai yksinkertaisuuksia . Heidän nimensä ovat ulottuvuusjärjestyksessä:
- 0. Piste
- 1. Linjasegmentti
- 2. Tasasivuinen kolmio (säännöllinen trigoni)
- 3. Tavallinen tetraedri
- 4. Säännöllinen pentakoroni tai 4-yksinkertaisuus
- 5. Säännöllinen heksateroni tai 5-yksinkertaisuus
- ... n -simplexissä on n +1 kärkeä .
Mittaa polytoopit (hyperkuutiot)

|
|

|
| Neliö | Kuutio | Tesseract |

|

|

|
Aloittaa seikasta . Laajenna viiva pisteeseen B etäisyydellä r ja yhdistä muodostaaksesi viivasegmentin. Laajenna toinen pituuden r , kohtisuoraan AB: n kanssa , pisteestä B kohtaan C ja samalla tavalla A: sta D: ksi , muodostaen neliön ABCD . Laajentaa riviä, joiden pituus on r vastaavasti kustakin kulmasta, on kohtisuorassa sekä AB ja BC (eli ylöspäin). Merkitse uudet pisteet E , F , G , H muodostaaksesi kuution ABCDEFGH . Ja niin korkeammille ulottuvuuksille.
Nämä ovat mittapolytooppeja tai hyperkuutioita . Heidän nimensä ovat ulottuvuusjärjestyksessä:
- 0. Piste
- 1. Linjasegmentti
- 2. Neliö (säännöllinen nelikulmio )
- 3. Kuutio (tavallinen heksahedroni)
- 4. Tesseract (tavallinen oktakoroni) tai 4-kuutio
- 5. Penteract (säännöllinen dekateroni) tai 5-kuutio
- ... n- kuutiossa on 2 n kärkeä .
Ristipolytoopit (ortoplexit)

|

|

|
| Neliö | Oktaedri | 16-soluinen |

|

|

|
Aloittaa seikasta O . Pidennä viivaa pisteisiin A ja B vastakkaisiin suuntiin etäisyyden r päässä O: sta ja 2 r: n päässä toisistaan. Piirrä viivan COD , jonka pituus on 2 r , keskellä O : ta ja kohtisuorassa AB: n kanssa . Yhdistä päät muodostaen neliönmuotoisen ACBD: n . Piirrä saman pituinen viiva EOF , jonka keskipiste on O: lla, kohtisuorassa AB: n ja CD: n kanssa (eli ylös ja alas). Yhdistä päät neliöön muodostaaksesi säännöllisen oktaedrin . Ja niin korkeammille ulottuvuuksille.
Nämä ovat ristipolytoopit tai ortoplexit . Heidän nimensä ovat ulottuvuusjärjestyksessä:
- 0. Piste
- 1. Linjasegmentti
- 2. Neliö (säännöllinen nelikulmio)
- 3. Säännöllinen oktaedri
- 4. Säännöllinen heksadekakoroni ( 16-solu ) tai 4-ortopleksi
- 5. Säännöllinen triacontakaiditeron ( Pentacross ) tai 5- ortoplex
- ... N- ortoplexissa on 2n kärkeä .
Löytöhistoria
Kuparit polygonit ja polyhedra
Aikaisin vakiintuneiden säännöllisten polygonien ja polyhedrojen matemaattinen käsittely tulee meille antiikin Kreikan matemaatikoilta. Viisi platonista kiinteää ainetta olivat heidän tiedossa. Pythagoras tiesi ainakin kolme heistä, ja Theaetetus (n. 417 eaa. - 369 eKr.) Kuvasi kaikkia viittä. Myöhemmin Euclid kirjoitti systemaattisen matematiikan tutkimuksen julkaisemalla sen nimellä Elements , joka rakensi loogisen teorian geometriasta ja lukuteoriasta . Hänen työnsä päättyi viiden platonisen kiinteän aineen matemaattisiin kuvauksiin .
Tähtien polygonit ja polyhedra
Ymmärryksemme pysyi staattisena monien vuosisatojen ajan Eukleidin jälkeen. Säännöllisten polytooppien myöhemmälle historialle voidaan luonnehtia peruskäsitteen asteittainen laajentuminen, jolloin yhä useammat kohteet voidaan ottaa huomioon niiden lukumäärässä. Thomas Bradwardine (Bradwardinus) nauhoitti ensimmäisenä vakavan tähtipolygonien tutkimuksen. Renessanssitaiteessa esiintyy erilaisia tähtipoledreja, mutta vasta Johannes Kepler tutki pieniä tähtikuvioisia dodekahedroneja ja suuria tähtikuvioisia dodekahedroneja vuonna 1619 ja huomasi näiden kahden olevan säännöllisiä. Louis Poinsot löysi suuren dodekaederin ja suuren ikosaedrin vuonna 1809, ja Augustin Cauchy osoittautui luettelon täydelliseksi vuonna 1812. Nämä polyhedrat tunnetaan yhtä lailla yhdessä kuin Kepler-Poinsot-polyhedra .
| Kepler-Poinsot-polyhedra | |||

|

|

|

|
| Pieni tähtikuvioitu dodekaedri |
Suuri tähtidodekaedri |
Suuri dodekaedri | Suuri ikosaedri |
Suuremman ulottuvuuden polytoopit
Vasta 1800-luvulla sveitsiläinen matemaatikko Ludwig Schläfli tutki ja luonnehti säännöllisiä polytooppeja korkeammissa mitoissa. Hänen työnsä julkaistiin ensimmäisen kerran kokonaisuudessaan julkaisussa Schläfli (1901) , kuusi vuotta postuumisti, vaikka osa siitä julkaistiin julkaisuissa Schläfli (1855) ja Schläfli (1858) . Vuosien 1880 ja 1900 välillä ainakin yhdeksän muuta matemaatikkoa löysi Schläflin tulokset itsenäisesti - katso lisätietoja Coxeteristä (1948 , s. 143–144) . Schläfli kutsui tällaista kuvaa "polyskemiksi" (englanniksi "polyscheme" tai "polyschema"). Termin "polytooppi" esitteli Reinhold Hoppe , yksi Schläflin uudelleen löytäjistä, vuonna 1882, ja Alicia Boole Stott käytti sitä ensin englanniksi parikymmentä vuotta myöhemmin. Termiä "polyhedroidit" käytettiin myös aikaisemmassa kirjallisuudessa (Hilbert, 1952).
Coxeter (1948) on luultavasti kattavin painettu käsittely Schläflin ja vastaavista tuloksista tähän mennessä. Schläfli osoitti, että on olemassa kuusi säännöllistä kuperaa polytooppia 4 ulottuvuudessa . Viisi niistä voidaan nähdä analogisina Platonin kiintoaineiden kanssa: 4-simplex (tai pentakoroni) tetraedriin , hyperkuutio (tai tesseract ) kuutioon , 4-ortoplex (tai heksadekachoroni tai 16-solu ) oktaedriin The 120-solu on dodekaedri , ja 600-solu on ikosaedri . Kuudennen, 24-solun , voidaan nähdä siirtymämuotona hyperkuution ja 16-solun välillä, analogisesti tapaan, jolla kuboktaedri ja rombinen dodekaedri ovat siirtymämuotoja kuution ja oktaedrin välillä.
Viidessä ja useammassa ulottuvuudessa on täsmälleen kolme säännöllistä polytooppia, jotka vastaavat tetraedonia , kuutiota ja oktaedonia : nämä ovat säännöllisiä yksinkertaisuuksia , mittaavat polytooppeja ja ristipolytooppeja . Näiden kuvaukset löytyvät tavallisten polytooppien luettelosta . Kiinnostavia ovat myös tähtien säännölliset 4-polytoopit , jotka Schläfli osittain löysi.
1800-luvun loppuun mennessä matemaatikot, kuten Arthur Cayley ja Ludwig Schläfli, olivat kehittäneet teorian säännöllisistä polytoopeista neljässä ja korkeammassa ulottuvuudessa, kuten tesseract ja 24-solu .
Jälkimmäisiä on vaikea (vaikkakaan mahdotonta) visualisoida, mutta ne säilyttävät kuitenkin alemman ulottuvuuden serkkujensa esteettisesti miellyttävän symmetrian. Tesseract sisältää 8 kuutiomainen soluja. Se koostuu kahdesta rinnakkain olevasta hypertasosta olevasta kuutiosta, joiden vastaavat kärjet on ristiin kytketty toisiinsa siten, että 8 poikittaista reunaa ovat pituudeltaan ja kohtisuorassa kuutiossa sijaitsevien 12 + 12 reunan kanssa. Kahden kuution vastaavat pinnat on yhdistetty muodostamaan loput 6 kuutio-pintaa tesseraktista . 24-solu voi olla peräisin tesseract liittymällä 8 kärjet kunkin sen tilavuuden kasvot ylimääräinen kärki muodostaa neljä-ulotteinen analoginen pyramidin. Molemmat kuvat, samoin kuin muut 4-ulotteiset kuviot, voidaan visualisoida ja kuvata suoraan 4-ulotteisilla stereografeilla.
Vaikeampi vielä kuvitella ovat nykyaikaisemmat abstraktit säännölliset polytoopit , kuten 57-solu tai 11-solu . Matemaattisesta näkökulmasta näillä esineillä on kuitenkin samat esteettiset ominaisuudet kuin tutuilla kahden ja kolmiulotteisilla sukulaisillaan.
1900-luvun alussa säännöllisen polytoopin määritelmä oli seuraava.
- Säännöllinen monikulmio on monikulmio, jonka reunat ovat kaikki samat ja jonka kulmat ovat samat.
- Säännöllinen monikulmio on monikulmio, jonka kasvot ovat kaikki yhteneväisiä säännöllisiä polygoneja ja jonka kärkiluvut ovat kaikki yhtäläiset ja säännölliset.
- Ja niin edelleen, säännöllinen n- polytooppi on n- ulotteinen polytooppi, jonka ( n - 1) -ulotteiset kasvot ovat kaikki säännöllisiä ja yhteneväisiä ja jonka kärkiluvut ovat kaikki säännöllisiä ja yhteneviä.
Tämä on "rekursiivinen" määritelmä. Se määrittelee korkeampiulotteisten kuvien säännöllisyyden alemman ulottuvuuden säännöllisten lukujen muodossa. On olemassa vastaava (ei-rekursiivinen) määritelmä, jonka mukaan polytooppi on säännöllinen, jos sillä on riittävä symmetria.
- N -polytope on säännöllinen, jos jokin joukko koostuu kärkipiste, reuna, joka sisältää sen, 2-ulotteinen kasvot, joka sisältää reunan, ja niin edelleen aina n -1 mitat, voidaan kuvata millä tahansa muulla tällaisella asettamat symmetriaa polytooppi.
Joten esimerkiksi kuutio on säännöllinen, koska jos valitsemme kuution kärjen ja yhden kolmesta reunasta, jossa se on, ja toinen kahdesta reunasta, jotka sisältävät reunan, tämä tripletti tai lippu (kärki, reuna, kasvot) voidaan kartoittaa mihin tahansa muuhun tällaiseen lippuun kuution sopivalla symmetrialla. Siten voimme määritellä säännöllisen polytoopin hyvin ytimekkäästi:
- Säännöllinen polytooppi on sellainen, jonka symmetriaryhmä on transitiivinen sen lipuissa.
1900-luvulla tapahtui joitain tärkeitä kehityskulkuja. Symmetria ryhmien klassisen säännöllisen polytooppeina oli yleistää mitä nyt kutsutaan Coxeter ryhmiä . Kokseteriryhmät sisältävät myös avaruuden tai tason säännöllisten tesselointien symmetriaryhmät . Esimerkiksi äärettömän shakkilaudan symmetriaryhmä olisi Coxeter-ryhmä [4,4].
Apeirotoopit - äärettömät polytoopit
1900-luvun alkupuolella Coxeter ja Petrie löysivät kolme ääretöntä rakennetta {4, 6}, {6, 4} ja {6, 6}. He kutsuivat heitä tavallisiksi vinoiksi polyhedeiksi, koska ne näyttivät täyttävän säännöllisen monikulmion määritelmän - kaikki kärjet, reunat ja pinnat ovat samanlaiset, kaikki kulmat ovat samat ja kuvassa ei ole vapaita reunoja. Nykyään niitä kutsutaan äärettömiksi polyhedeiksi tai apeirohedroiksi. Tasojen {4, 4}, {3, 6} ja {6, 3} säännöllisiä vierekkäisyyksiä voidaan myös pitää äärettöminä polyhedeinä.
1960-luvulla Branko Grünbaum kehotti geometrista yhteisöä harkitsemaan abstraktimpia tyypillisiä säännöllisiä polytooppeja, joita hän kutsui polystromatoiksi . Hän kehitti polystromatateorian esittelemällä esimerkkejä uusista esineistä, joita hän kutsui säännöllisiksi apeirotoopeiksi , toisin sanoen säännöllisiksi polytoopeiksi , joilla on äärettömän monta kasvoa. Yksinkertainen esimerkki vinosta apeirogonista olisi siksak. Se näyttää täyttävän säännöllisen monikulmion määritelmän - kaikki reunat ovat saman pituisia, kaikki kulmat ovat samat ja kuvassa ei ole löysiä päitä (koska niihin ei koskaan pääse). Vielä tärkeämpää on ehkä siksak-symmetria, joka voi kartoittaa minkä tahansa kärkiparin ja kiinnitetyn reunan parin mihin tahansa. Siitä lähtien muita säännöllisiä apeirogoneja ja korkeampia apeirotooppeja on edelleen löydetty.
Säännölliset monimutkaiset polytoopit
Kompleksiluku on todellinen osa, joka on vähän me kaikki tiedämme, ja imaginaariosa, joka on moninkertainen neliöjuuri miinus yksi. Kompleksisen Hilbert-avaruuden koordinaatit x, y, z jne. Ovat kompleksilukuja. Tämä kaksinkertaistaa mittojen lukumäärän. Tällaiseen yhtenäiseen tilaan rakennettua polytooppia kutsutaan monimutkaiseksi polytoopiksi .
Abstraktit polytoopit

Grünbaum myös löysi 11-solu , neljän ulotteinen itsensä dual esine, jonka puolia eivät icosahedra, mutta ovat "hemi-icosahedra" - eli ne ovat muodoltaan kukaan, jos otetaan huomioon vastakkaisille puolille icosahedra olevan todella sama kasvot ( Grünbaum 1976 ). Hemi-ikosaedrilla on vain 10 kolmiopintaa ja 6 kärkeä, toisin kuin ikosaedrilla, jolla on 20 ja 12.
Tämän käsitteen voi olla helpompi ymmärtää lukijalle, jos otetaan huomioon kuution ja hemikubin suhde. Tavallisessa kuutiossa on 8 kulmaa, ne voidaan merkitä A: sta H: seen, A: lla H: tä vastapäätä, B: llä G: tä vastapäätä ja niin edelleen. Hemikubissa A: ta ja H: ta kohdellaan samalla kulmana. Niin tekisivät B ja G ja niin edelleen. Reunasta AB tulee sama reuna kuin GH, ja ABEF: n kasvosta tulee sama pinta kuin CDGH: sta. Uudessa muodossa on vain kolme pintaa, 6 reunaa ja 4 kulmaa.
11-solua ei voida muodostaa säännöllisellä geometrialla tasaisessa (euklidisessa) hyperavaruudessa, mutta vain positiivisesti kaarevassa (elliptisessä) hyperavaruudessa.
Muutama vuosi sen jälkeen, kun Grünbaum löysi 11-solun , HSM Coxeter löysi itsenäisesti saman muodon. Hän oli aiemmin löytänyt samanlaisen polytoopin, 57-solun (Coxeter 1982, 1984).
Vuoteen 1994 mennessä Grünbaum harkitsi polytooppeja abstraktisti yhdistelmäpisteinä tai pisteinä, eikä ollut huolissaan siitä, olivatko kasvot tasomaisia. Kun hän ja muut puhdistivat näitä ideoita, tällaisia sarjoja alettiin kutsua abstrakteiksi polytoopeiksi . Abstrakti polytooppi määritellään osittain järjestetyksi joukoksi (poset), jonka elementit ovat polytoopin kasvot (kärjet, reunat, kasvot jne.), Jotka on järjestetty eristämisen avulla . Joukolle asetetaan tiettyjä rajoituksia, jotka ovat samanlaisia kuin perinteisten säännöllisten polytooppien (mukaan lukien platoniset kiinteät aineet) täyttämät ominaisuudet. Rajoitukset ovat kuitenkin tarpeeksi löysät, että säännölliset tessellaatiot, hemikuutiot ja jopa niin outoja esineitä kuin 11-soluiset tai muukalaiset ovat kaikki esimerkkejä tavallisista polytoopeista.
Geometrisen polytoopin ymmärretään olevan abstraktin polytoopin toteutus siten, että abstrakteista elementeistä geometriseen kuvantaminen tapahtuu yksi kerrallaan. Siten mikä tahansa geometrinen polytooppi voidaan kuvata sopivalla abstraktilla posetilla, vaikka kaikilla abstrakteilla polytoopeilla ei ole asianmukaista geometrista toteutusta.
Teoriaa on sittemmin kehitetty edelleen, lähinnä McMullen & Schulte (2002) , mutta myös muut tutkijat ovat antaneet panoksensa.
Abstraktien polytooppien säännöllisyys
Säännöllisyydellä on toisiinsa liittyvä, tosin erilainen merkitys abstrakteille polytoopeille , koska kulmilla ja reunojen pituuksilla ei ole merkitystä.
Johdannossa annettua määritelmää säännöllisyydestä lippujen transitiivisuuden suhteen sovelletaan abstrakteihin polytoopeihin.
Kaikilla klassisilla säännöllisillä polytoopeilla on abstrakti vastine, joka on säännöllinen, saatu ottamalla joukko kasvoja. Mutta epäsäännöllisillä klassisilla polytoopeilla voi olla säännöllisiä abstrakteja vastineita, koska abstraktit polytoopit eivät välitä esimerkiksi kulmista ja reunan pituuksista. Ja säännöllinen abstrakti polytooppi ei ehkä ole toteutettavissa klassisena polytooppina.
Kaikki polygonit ovat säännöllisiä esimerkiksi abstraktissa maailmassa, kun taas vain ne, joilla on samat kulmat ja saman pituiset reunat, ovat säännöllisiä klassisessa maailmassa.
Abstraktien polytooppien huippupiste
Huippuhahmon käsite määritellään myös eri tavalla abstraktille polytoopille . Tietyn abstraktin n- polytoopin kärkipiste tietyssä kärkipisteessä V on joukko kaikkia abstrakteja pintoja, jotka sisältävät V: n , mukaan lukien itse V. Muodollisemmin se on abstrakti osa
- F n / V = { F | V ≤ F ≤ F n }
missä F n on suurin pinta eli nimellinen n- pinta, joka sisältää kaikki muut kasvot. Huomaa, että jokaisesta alkuperäisen polytoopin i- pinnasta, i ≥ 0, tulee ( i - 1) -piste huippupisteestä.
Toisin kuin euklidisilla polytoopeilla, abstrakti polytooppi, jossa on säännölliset puolet ja kärkihahmot, voi olla itse tai säännöllinen - esimerkiksi neliön muotoinen pyramidi, jonka kaikki puolet ja kärkipisteet ovat säännöllisiä abstrakteja polygoneja.
Klassinen kärkihahmo on kuitenkin abstraktin oivallus.
Rakenteet
Monikulmioita
Perinteinen tapa rakentaa säännöllinen polygoni tai jokin muu hahmo tasossa on kompassilla ja suoralla . Joidenkin säännöllisten polygonien rakentaminen tällä tavalla on hyvin yksinkertaista (helpoin on ehkä tasasivuinen kolmio), jotkut ovat monimutkaisempia ja jotkut mahdottomia ("ei rakennettavissa"). Yksinkertaisia muutamia säännöllisiä polygoneja, joita on mahdotonta muodostaa, ovat n- puoliset polygonit, joiden n on 7, 9, 11, 13, 14, 18, 19, 21, ...
Rakennettavuus viittaa tässä mielessä vain ihanteellisiin rakenteisiin, joissa on ihanteelliset työkalut. Tietenkin kohtuullisen tarkat likiarvot voidaan rakentaa useilla menetelmillä; vaikka teoreettisesti mahdolliset rakenteet voivat olla epäkäytännöllisiä.
Polyhedra
Eukleidin elementit antoivat viivain- ja kompassirakenteille viiden platonisen kiinteän aineen määrän. Pelkästään käytännöllinen kysymys siitä, miten avaruuteen voidaan piirtää suora viiva, jopa viivaimen kanssa, saattaa kuitenkin herättää kysymyksen, mitä tarkalleen tarkoittaa tavallisen monikulmion "rakentaminen". (Tietysti voitaisiin esittää sama kysymys monikulmioista.)
Englanninkielisellä sanalla "construct" on merkitys, että asia rakennetaan järjestelmällisesti. Yleisin tapa esittää säännöllinen monikulmio on taitettavan verkon kautta . Saadaaksesi taitettava verkko polykedristä, otetaan monikulmion pinta ja leikataan se vain niin monta reunaa pitkin, että pinta voidaan asettaa tasaiseksi. Tämä antaa suunnitelman avautuneen monikulmion verkosta. Koska platonilaisilla kiinteillä aineilla on vain kolmioita, neliöitä ja viisikulmioita kasvoille, ja nämä kaikki ovat rakennettavissa viivaimen ja kompassin kanssa, on olemassa viivaimen ja kompassin menetelmiä näiden taitettavien verkkojen vetämiseksi. Sama pätee tähtipoledereihin, vaikka tässä onkin varottava, että verkko tehdään vain näkyvälle ulkopinnalle.
Jos tämä verkko vedetään pahville tai vastaavalle taitettavalle materiaalille (esimerkiksi pelti), verkko voidaan leikata, taittaa leikkaamattomia reunoja pitkin, liittää sopivia leikattuja reunoja pitkin ja muodostaa siten polyhedron, jolle verkko on tarkoitettu suunniteltu. Tietyn monikulmion kohdalla voi olla monia taitettavia verkkoja. Esimerkiksi kuutioon on 11 ja dodekaedrille yli 900000.
Lukuisat lasten lelut, jotka on yleensä suunnattu teini- tai teini-ikäisille ikäryhmille, mahdollistavat kokeilun säännöllisten monikulmioiden ja polyhedrien kanssa. Esimerkiksi klikko tarjoaa sarjaa muovisia kolmioita, neliöitä, viisikulmioita ja kuusikulmioita, jotka voidaan liittää reunasta reunaan useilla eri tavoilla. Tällaisella lelulla leikkivä lapsi voi löytää uudelleen Platonin kiintoaineet (tai Archimedeksen kiinteät aineet ), varsinkin jos hänelle annetaan vähän tietoa asiantuntevalta aikuiselta.
Teoriassa melkein mitä tahansa materiaalia voidaan käyttää säännöllisen polyhedran rakentamiseen. Ne voidaan veistää puusta, mallia langasta, muodostua lasimaalauksista. Mielikuvitus on raja.
Suuremmat mitat


Korkeammissa ulottuvuuksissa on vaikeampi sanoa, mitä tarkoitetaan "rakentamalla" esineitä. Kolmiulotteisessa maailmankaikkeudessa on selvää, että on mahdotonta rakentaa fyysistä mallia esineestä, jolla on vähintään 4 ulottuvuutta. Tämän ongelman voittamiseksi käytetään yleensä useita lähestymistapoja.
Ensimmäinen lähestymistapa, joka soveltuu neljälle ulottuvuudelle, käyttää nelidimensionaalista stereografiaa. Kolmannen ulottuvuuden syvyys esitetään vaakasuoralla suhteellisella siirtymällä, syvyys neljännellä mitalla pystysuoralla suhteellisella siirtymällä stereografian vasemman ja oikean kuvan välillä.
Toinen lähestymistapa on upottaa korkeampiulotteiset objektit kolmiulotteiseen avaruuteen käyttäen menetelmiä, jotka ovat analogisia tapojen kanssa, joilla kolmiulotteiset objektit piirretään tasolle. Esimerkiksi edellisessä osassa mainituilla taitetuilla verkoilla on korkeampi ulottuvuus. Voidaan jopa kuvitella rakentavansa mallin tästä taitettavasta verkosta, kun piirretään monikulmion taitettava verkko paperille. Valitettavasti emme koskaan voineet tehdä tarvittavaa kolmiulotteisen rakenteen taittamista 4-ulotteisen polytoopin saamiseksi fyysisen maailmankaikkeuden rajoitusten vuoksi. Toinen tapa "piirtää" korkeampiulotteisia muotoja kolmessa ulottuvuudessa on jonkinlainen projektio, esimerkiksi joko ortografisen tai perspektiivisen projektion analogi . Coxeterin kuuluisassa kirjassa polytoopeista ( Coxeter 1948 ) on joitain esimerkkejä tällaisista oikolukuennusteista. Huomaa, että jopa 4-ulotteisen polykoran upottaminen suoraan kahteen ulottuvuuteen on melko hämmentävää. Kolmiulotteiset mallit ennusteista ovat helpommin ymmärrettävissä. Tällaisia malleja löytyy toisinaan tiedemuseoista tai yliopistojen matematiikan osastoilta (kuten Université Libre de Bruxelles ).
Neljän (tai korkeamman) ulotteisen säännöllisen polytoopin ja kolmiulotteisen hypertason leikkauspiste on polytooppi (ei välttämättä säännöllinen). Jos hypertasoa liikutetaan muodon läpi, kolmiulotteiset viipaleet voidaan yhdistää, animoida eräänlaiseksi nelidimensionaaliseksi kohteeksi, jossa neljännen ulottuvuuden pidetään olevan aika. Tällä tavoin voimme nähdä (ellei täysin ymmärrä) neljänulotteisten säännöllisten polytooppien koko neliöulotteisen rakenteen sellaisten leikkausten läpi. Tämä on analoginen tapaan, jolla CAT-skannaus kokoaa uudelleen kaksiulotteiset kuvat muodostaen kolmiulotteisen kuvan skannattavista elimistä. Ihanteellinen olisi jonkinlainen animoitu hologrammi , mutta jopa yksinkertainen animaatio, kuten esitetty, voi jo antaa rajoitetun käsityksen polytoopin rakenteesta.
Toinen tapa, jolla kolmiulotteinen katsoja voi ymmärtää neliulotteisen polytoopin rakenteen, on "uppoutuminen" esineeseen, kenties jonkinlaisen virtuaalitodellisuustekniikan avulla. Ymmärtääksesi, miten tämä voi toimia, kuvittele, mitä voisi nähdä, jos tila olisi täynnä kuutioita. Katsoja olisi yhden kuution sisällä ja pystyisi näkemään kuutioita itsensä edessä, takana, yläpuolella, alapuolella, vasemmalla ja oikealla puolella. Jos voisi matkustaa näihin suuntiin, voitaisiin tutkia kuutioiden joukkoa ja saada käsitys sen geometrisesta rakenteesta. Ääretön joukko kuutiot ei polytooppi perinteisessä mielessä. Itse asiassa se on kolmiulotteisen ( euklidisen ) avaruuden tessellaatio . Kuitenkin, 4-polytooppia voidaan pitää mosaiikki 3-ulotteinen ei-Euclidean tilan, nimittäin mosaiikki pinnan neljän-ulotteinen pallo (4-ulotteisen pallomainen laatoitus ).
Paikallisesti tämä tila näyttää tutulta, ja siksi virtuaalitodellisuusjärjestelmä voitaisiin periaatteessa ohjelmoida sallimaan näiden "tesselaatioiden" eli 4-ulotteisten säännöllisten polytooppien tutkiminen. Matematiikan osasto UIUC on useita kuvia mitä voisi nähdä, jos upotettu mosaiikki on hyperbolinen tilaa kanssa dodecahedra. Tällainen tessellaatio on esimerkki äärettömästä abstraktista säännöllisestä polytoopista.
Normaalisti abstraktien säännöllisten polytooppien kohdalla matemaatikko katsoo, että kohde on "rakennettu", jos sen symmetriaryhmän rakenne tiedetään. Tämä johtuu abstraktien säännöllisten polytooppien tutkimisessa olevasta tärkeästä lauseesta, joka tarjoaa tekniikan, joka sallii abstraktin säännöllisen polytoopin rakentamisen symmetriaryhmästä standardilla ja suoraviivaisella tavalla.
Säännölliset polytoopit luonnossa
Katso esimerkkejä luonnon monikulmioista:
Kukin platoninen kiinteä aine esiintyy luonnollisesti yhdessä tai toisessa muodossa:
Katso myös
Viitteet
Huomautuksia
Bibliografia
- Coxeter, HSM (1973). Säännölliset polytoopit (3. painos). Dover. ISBN 0-486-61480-8.
- - (1974). Säännölliset monimutkaiset polytoopit . Cambridge University Press. ISBN 052120125X.
- - (1991). Säännölliset kompleksiset polytoopit (2. painos). Cambridge University Press. ISBN 978-0-521-39490-1.
- Cromwell, Peter R. (1999). Polyhedra . Cambridge University Press. ISBN 978-0-521-66405-9.
- Euclid (1956). Elementit . Kääntäjä Heath, TL Cambridge University Press.
- Grünbaum, B. (1976). Kuvaajien, kompleksien ja mallien säännöllisyys . Problèmes Combinatoires et Théorie des Graphes, Colloquium Internationale CNRS, Orsay. 260 . s. 191–197.
- Grünbaum, B. (1993). "Ontto pintainen polyhedra". Julkaisussa Bisztriczky, T .; et ai. (toim.). POLYTOPIT: abstraktit, kuperat ja laskennalliset . Matemaattiset ja fyysiset tieteet, Naton syventävä tutkimusinstituutti. 440 . Kluwer Academic. s. 43–70. ISBN 0792330161.
- McMullen, P .; Schulte, S. (2002). Abstraktit säännölliset polytoopit . Cambridge University Press.
- Sanford, V. (1930). Lyhyt matematiikan historia . Riverside Press.
- Schläfli, L. (1855). "Réduction d'une intégrale multiple, qui comprend l'arc de cercle et l'aire du triangle sphérique comme cas particuliers". Journal de Mathématiques . 20 : 359–394.
- Schläfli, L. (1858). "Useilla integraaleilla ∫ ^ n dxdy ... dz, joiden rajat ovat p_1 = a_1x + b_1y +… + h_1z> 0, p_2> 0, ..., p_n> 0 ja x ^ 2+ y ^ 2 +… + z ^ 2 <1 ". Neljännesvuosittainen lehti puhtaasta ja sovelletusta matematiikasta . 2 : 269–301. 3 (1860) s. 54–68, 97–108.
- Schläfli, L. (1901). "Theorie der vielfachen Kontinuität". Denkschriften der Schweizerischen Naturforschenden Gesellschaft . 38 : 1–237.
- Smith, JV (1982). Geometrinen ja rakenteellinen kristallografia (2. painos). Wiley. ISBN 0471861685.
- Van der Waerden, BL (1954). Tiede herää . Kääntäjä Dresden, Arnold. P Noordhoff.
- DMY Sommerville (2020) [1930]. "X. Säännölliset polytoopit" . Johdanto n- ulottuvuuksien geometriaan . Courier Dover. s. 159–192. ISBN 978-0-486-84248-6.
Ulkoiset linkit
- Olshevsky, George. "Säännöllinen polytooppi" . Hyperspace-sanasto . Arkistoitu alkuperäisestä 4. helmikuuta 2007.
- Pienten säännöllisten polytooppien atlas - Luettelo abstrakteista säännöllisistä polytoopeista.